백준 1365 전깃줄 /LIS (최장 증가 부분 수열)

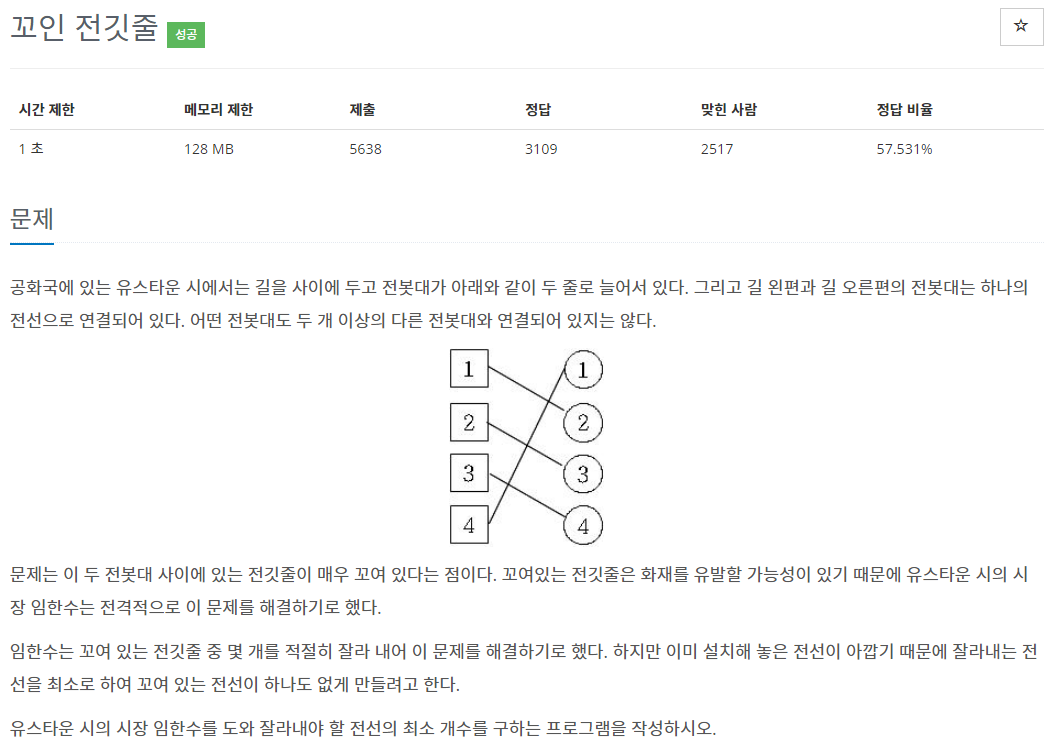
문제 

https://www.acmicpc.net/problem/1365

 

---

Summary

제공된 수열에서 오름차순으로 정렬된 가장 긴 부분 수열을 찾는 알고리즘
LIS 의 경우 연속적으로 연결되거나 할 필요없이 오름 차순 상으로 연결되있으면 성립됨.

 

---

목표

• DP로 푸는게 가능하지만 여기서는 Lower_Bound방식으로 제작 (N^2 -> NLogN)
• Binary Search 부분 분리 및 코드 리팩토링

 

---

Solution

• Given

    private int N;
    private int[] linked;
    private int[] arr;

 

 

• When

        int lastIdx = 0;
        for(int i=0; i<N; i++) {
            // add last value
            if (arr[lastIdx] < linked[i]) {
                arr[++lastIdx] = linked[i];
                continue;
            }
			
            // Search & Change
            int idx = findIdx(linked[i], 0, lastIdx);
            arr[idx] = linked[i];
        }

        int cnt = 0;
        for (int k = 0; k < N; k++) {
            if (arr[k] == 0) continue;
            cnt +=1;
        }

 

• Function - findIdx ( Change 되는 Index를 이진탐색 )  

    private int findIdx(int target, int start, int last) {
        int mid, value;
        while (start <= last) {
            mid = (start + last) / 2;
            value = arr[mid];

            if (value < target) start = mid +1;
            else last = mid -1;
        }
        return start;
    }

 

• Then

        System.out.println(N - cnt);